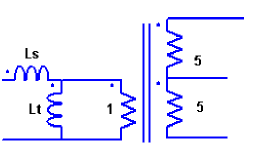
漏れインダクタンス

漏れインダクタンス（もれいんだくたんす）または、漏洩インダクタンス（ろうえいいんだくたんす）または、リーケージインダクタンス（英: Leakage inductance）は、変圧器（トランス）において、一次巻線と二次巻線との結合係数が小さい場合に、変圧器を構成する巻線の一部が変圧作用に寄与せず、チョークコイルと等価な成分となって生じるものをいう。一次巻線と二次巻線とが完全な結合をした（結合係数k=1の）理想変圧器の場合、漏れインダクタンスの値はゼロである。しかし、一般的な変圧器の場合は結合係数が1以下であり、結合が完全でないことから巻線の一部がインダクタンスとして働く。等価回路上では、漏れインダクタンスは変圧器の一次巻線、または二次巻線に直列にチョークコイルL_eが接続されたものとして表される。

漏れインダクタンスには電気学会で定義されるものと工業会の測定法として定められるものと二つある。

漏れインダクタンスの発生

変圧器の磁束

変圧器の一次巻線と二次巻線の双方と鎖交する磁束を主磁束(φ₁₂またはφ₂₁)という。変圧器の磁束はこの他に、一次巻線だけと鎖交し二次巻線とは鎖交しない一次側漏れ磁束(φ_σ1)と、二次巻線とだけ鎖交し、一次巻線とは鎖交しない二次側漏れ磁束(φ_σ2)とがある。理想的な変圧器の場合は主磁束のみしか存在しないが、実際の変圧器には磁気漏れがあるので必ず漏れ磁束が存在する。そして、この漏れ磁束は一次側、二次側、それぞれの巻線のみしか鎖交しないために、変圧作用には寄与しない。また同時に、それぞれの巻線のみしか鎖交しないということはそれぞれの巻線のインダクタンスとして寄与していることを意味する。このようにして、一次側漏れ磁束は一次側漏れインダクタンスとなり、二次側漏れ磁束は二次側漏れインダクタンスとなる。

結合係数をkとして、一次巻線の自己インダクタンスをL₁、二次巻線の自己インダクタンスを L₂とすれば、それぞれの漏れインダクタンスは、

L_{\mathrm {e1} }=(1-k)\cdot L_{\mathrm {1} }\,

L_{\mathrm {e2} }=(1-k)\cdot L_{\mathrm {2} }\,

となる。

三端子等価回路

変圧器の等価回路では漏れインダクタンスを一次側、或いは二次側に、理想変圧器を介してインピーダンス変換し、相互インダクタンスとともに記載する。これを三端子等価回路という。三端子等価回路で表される変圧器の等価回路では、この一次側漏れインダクタンスL_e1と二次側漏れインダクタンスL_e2とは同じ値を持つ。これが電気学会で定義される漏れインダクタンスL_eである。

漏れインダクタンスの実測

工業会で実測的に定めた漏れインダクタンスL_scは変圧器の一次巻線、または二次巻線を短絡して、他方から実測することにより求められる。このL_scを工業会で実測的に定めた漏れインダクタンスという。短絡インダクタンスともいう。電気学会定義の漏れインダクタンスとは値が異なる。

実測したL_openとL_scから結合係数ｋが得られる。

k={\sqrt {1-{\frac {L_{\mathrm {sc} }}{L_{\mathrm {open} }}}}}

二次巻線を短絡して一次巻線を計測して得られるインダクタンスを一次側漏れインダクタンスL_sc1という。また、一次巻線を短絡して二次巻線を計測して得られるインダクタンスを二次側漏れインダクタンスL_sc2という。これらの値とそれぞれの巻線の自己インダクタンスとにより計算した結合係数kは、一次側から測っても二次側から測っても全く同じ値にならなければならない。

L等価回路（簡易等価回路）

より実用的な表記法として、漏れインダクタンスを一次側あるいは二次側にまとめて表記した方法もある。等価回路的には漏れインダクタンスを一次側に配置しても二次側に配置しても、それぞれを巻数比（変成比）によってインピーダンス変換すると同じ結果になる。

L_{\mathrm {sc2} }=L_{\mathrm {sc1} }\cdot \left({\frac {N_{2}}{N_{1}}}\right)^{2}

L_{\mathrm {sc1} }=L_{\mathrm {sc2} }\cdot \left({\frac {N_{1}}{N_{2}}}\right)^{2}

この場合の漏れインダクタンスL_scは変圧器の一次巻線または二次巻線に直列に接続されたチョークコイルと等価な働きをする。回路設計上においては、工業会で実測的に定めた漏れインダクタンス(短絡インダクタンス)の方がより実用的である。
それぞれの巻線の自己インダクタンスをL₁ 、L₂ として結合係数をk とすれば、工業会で実測的に定めた漏れインダクタンスL_sc は、

L_{\mathrm {sc1} }=(1-k^{2})\cdot L_{\mathrm {1} }\,

L_{\mathrm {sc2} }=(1-k^{2})\cdot L_{\mathrm {2} }\,

となる。

補足

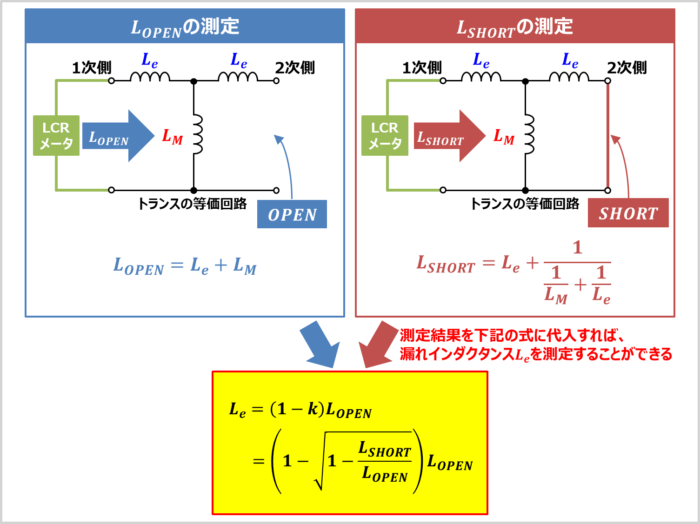
工業会で実測的に定めた漏れインダクタンス(短絡インダクタンス)L_scと電気学会定義の漏れインダクタンスL_eとの関係は以下のようになる。

L_{\mathrm {sc1} }=(1 k)\cdot L_{\mathrm {e1} }\,

L_{\mathrm {sc2} }=(1 k)\cdot L_{\mathrm {e2} }\,

漏れインダクタンスの利用

漏れインダクタンスを利用する際、実際には漏れインダクタンスL_eを直接利用することはなく理論的に登場するのみである。直接的に利用される数値は工業会で実測的に定めた漏れインダクタンス（短絡インダクタンス）L_scの方である。一般に、変圧器の漏れインダクタンスは変圧器の出力電圧を下げる要素として好ましくないとされるが、電流が流れると電圧が下がる性質を積極的に利用して、変圧器に大きな漏れインダクタンスを持たせたものが、主に負性抵抗特性を有する蛍光灯やネオン灯、その他放電灯の電流安定器、アーク溶接の安定器、電子レンジのマグネトロンの安定器などに応用される。磁気漏れ変圧器の用途は多彩である。

また、二次巻線に並列に共振コンデンサを接続し、二次側の短絡インダクタンスと容量成分とを共振させた共振変圧器は、蛍光灯電子安定器（インバータ）、ネオン灯電子安定器、冷陰極管用インバータや、テスラコイルなどに応用される。また、近年研究が進むワイヤレス電力伝送の動作解析においても電気学会定義の漏れインダクタンスL_eと短絡インダクタンスL_scはともに効率、性能、共振周波数などを決める重要なパラメータとなっている。