標準偏差

標準偏差（ひょうじゅんへんさ、（英: standard deviation, SD）とは、データや確率変数の、平均値からの散らばり具合（ばらつき）を表す指標の一つである。偏差ベクトルと、値が標準偏差のみであるベクトルは、ユークリッドノルムが等しくなる。

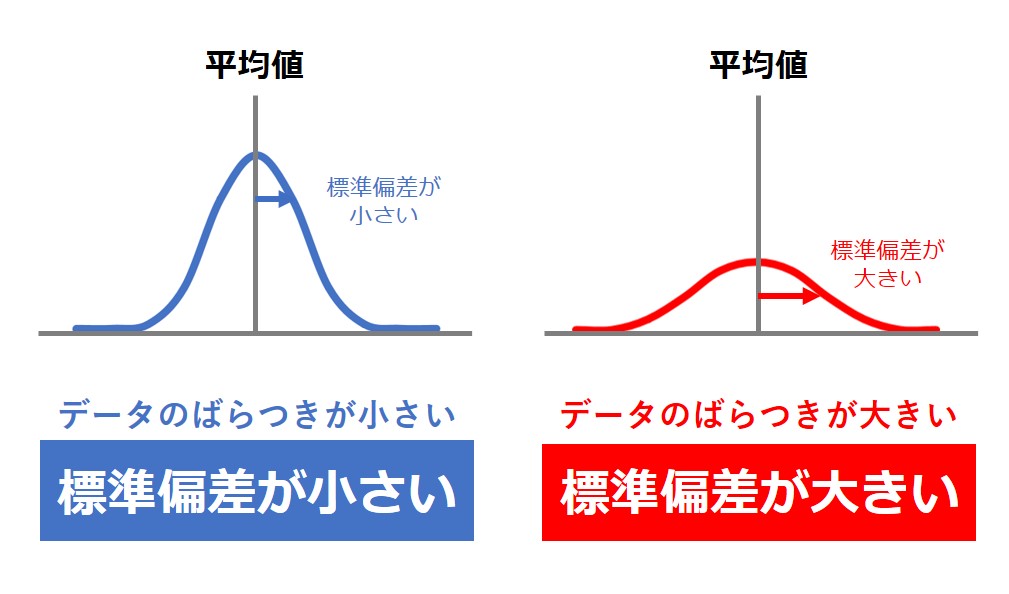
標準偏差を2乗したのが分散であり、従って、標準偏差は分散の非負の平方根である。標準偏差が 0 であることは、データの値が全て等しいことと同値である。

母集団や確率変数の標準偏差を σ で、標本の標準偏差を s で表すことがある。

二乗平均平方根 (RMS) を用いると、標準偏差は偏差の二乗平均平方根に等しくなる。

概要

データ x₁, x₂, …, x_n の平均値からの散らばり具合を数値にした標準偏差は、次の式で定義される：

${\displaystyle s={\sqrt {{\frac {1}{n}}\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}}$

ここで x は平均値を表す。この定義は、データを数ベクトルと見て、「散らばり具合」を偏差ベクトルのユークリッドノルムととらえる考えに基づく（このことより平均偏差でなく自乗平均をとる）。

もとのデータ x を、平均値、「散らばり具合」を変えず、偏差が全て同じであるように取り直したデータ y を考える。

x の大きさが奇数のときは、x を、自分自身2個を併せたデータ（大きさは偶数）に取り直す（そうしても平均値、「散らばり具合」は変わらない）。

y の偏差ベクトルは (±s, ±s, …, ±s) (s ≥ 0) の形になる。x と y の「散らばり具合」が等しいことから、

${\displaystyle \|{\boldsymbol {x}}-{\overline {\boldsymbol {x}}}\|=\|(\pm s,\cdots ,\pm s)\|}$

${\displaystyle ns^{2}=\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$

${\displaystyle s={\sqrt {{\frac {1}{n}}\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}}$ //

標準偏差は平方根を取るため、簡単な計算法則が成り立ちにくいという特徴がある。そこで分散 s² を

${\displaystyle s^{2}={\frac {1}{n}}\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$

で定義する。分散には簡単な計算法則がいくつか成り立つことから、種々の標準偏差ができるようになる。

標準偏差の概念は、イギリスの統計学者フランシス・ゴルトンにより、親子の身長の相関関係を調べる中で初めて見出された。データを数ベクトルと見る考え方は相関係数の導入と命名につながった。ゴルトンはこれらの研究により平均への回帰という現象を見出した。

ユニヴァーシティ・カレッジ・ロンドンのゴルトン研究室を継承したカール・ピアソンはゴルトンの研究を定式化、体系化し、初めて "standard deviation"（「標準偏差」）と名付けた。

確率分布において最も基本となる正規分布曲線において、変曲点の x座標と平均の絶対差は標準偏差に等しくなる。このことから、標準偏差は信頼区間の基本的な単位となる。

日本の受験業界で広く使われている学力偏差値は標準偏差の応用例の一つで、異なる試験でも、平均点よりどれだけ離れているかをある統一した尺度でとらえることができるようになっている。

金融工学においては、株式のリスクを確率分布の標準偏差でとらえることがある。

母集団の標準偏差

母集団全てのデータ x₁, x₂, …, x_n に対して、平均値 x は次の式で定義される：

${\displaystyle {\overline {x}}={\frac {1}{n}}\textstyle \sum \limits _{i=1}^{n}x_{i}}$

この平均値 x を使って得られる分散 σ² を次の式で定義する：

${\displaystyle \sigma ^{2}={\frac {1}{n}}\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}={\dfrac {1}{n}}\sum \limits _{i=1}^{n}{x_{i}}^{2}-{\overline {x}}^{2}}$

σ² を母分散と言うこともある。

この分散の非負の平方根 σ を、母集団の標準偏差と定義する。分散もデータの散らばり具合を表す統計量であるが、分散と違い標準偏差はデータの値と次元が等しくなる。偏差は平均的には標準偏差の分だけ離れていると考えることができる。

標本の標準偏差

標本標準偏差

母集団の中から、大きさ n（母集団の大きさよりはるかに小さい）の標本 x₁, x₂, …, x_n を抽出したとする。このとき、標本平均は次の式で表される：

${\displaystyle {\bar {x}}={\frac {1}{n}}\textstyle \sum \limits _{i=1}^{n}x_{i}}$

この標本平均を使って次式で定義される量を標本分散と呼ぶ：

${\displaystyle s^{2}={\frac {1}{n}}\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}={\dfrac {1}{n}}\sum \limits _{i=1}^{n}{x_{i}}^{2}-{\bar {x}}^{2}}$

標本分散の平方根 s を標本標準偏差と呼ぶ。

不偏標準偏差

σ² を母分散、s² を標本分散とすると、標本分散の期待値 E[s²] は、

${\displaystyle E[s^{2}]={\frac {n-1}{n}}\sigma ^{2}}$

となることが示される。つまり、標本分散は母分散よりも少し小さくなる。そのため、標本分散は母分散の不偏推定量ではない。そこで、

${\displaystyle v^{2}={\frac {1}{n-1}}\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}={\dfrac {1}{n-1}}\sum \limits _{i=1}^{n}{x_{i}}^{2}-{\dfrac {n}{n-1}}{\bar {x}}^{2}}$

を考えると、この量の期待値は母分散に等しく、母分散の不偏推定量になっている。

こうして定義される v² を不偏分散という。v を不偏標準偏差という。

紛らわしいが、 v² を標本分散と呼ぶこともある。さらに v² の平方根 v を標本標準偏差ということもある。名称の混乱については後述する。

母集団の標準偏差の不偏推定量

前述のように不偏分散は、母分散の不偏推定量である（標本から測定した推定量の期待値が母分散に等しい）。しかし、不偏分散の平方根 v は、母集団の標準偏差の不偏推定量ではない。

母集団が正規分布に従う場合、母集団の標準偏差の不偏推定量 D は次式で与えられる：

${\displaystyle D={\sqrt {\frac {n-1}{2}}}{\frac {\Gamma \left({\frac {n-1}{2}}\right)}{\Gamma \left({\frac {n}{2}}\right)}}v}$

ここで、Γ はガンマ関数、v² は不偏分散である。

標本の大きさが大きくなれば、母集団の標準偏差の不偏推定量 D は、近似的に、平均からの偏差平方和を n − 1.5 で割った値の平方根として求められる：

${\displaystyle D\approx {\sqrt {{\frac {1}{n-1.5}}\textstyle \sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}={\sqrt {{\dfrac {1}{n-1.5}}\textstyle \sum \limits _{i=1}^{n}{x_{i}}^{2}-{\dfrac {n}{n-1.5}}{\bar {x}}^{2}}}}$

名称の混乱

統計の教科書によっては、不偏分散（分母が n − 1 の方）を「標本分散」と呼んでいる場合もあり、用語が混乱して使用されている場合がある。母平均が不明で、代わりに標本平均を使用する場合には、期待値が母分散となる不偏分散を使用することが多い。

英語

英語では不偏分散による標準偏差のことを「sample standard deviation」（標本標準偏差）と呼ぶことが多い。この語はカール・ピアソンによって1893年に導入された。ただし不偏分散による標準偏差を意味する英語の表現には混乱がある。

• 英語版ウィキペディアの「standard deviation」という記事では、不偏分散による標準偏差（平均からの偏差平方和を n − 1 で割った値の平方根）のことを「corrected sample standard deviation」と表記し、平均からの偏差平方和を n で割った値の平方根を「uncorrected sample standard deviation」や「the standard deviation of the sample」と表記している。
• アメリカの Fundamentals of Engineering (FE) の試験問題での「sample standard deviation」は n − 1 で割る方を意味する。
• アメリカ・ユタ大学のトム・マロイは、統計学の学習者向けウェブページでは、「sample standard deviation」を平均からの偏差平方和を n で割った値の平方根だと解説している。

日本語

日本語の「不偏標準偏差」という語にも混乱がある。日本の大学教授の間でも、不偏分散 v² の平方根を、不偏標準偏差だと教える大学教員も多いが、母集団の標準偏差の不偏推定量 D を不偏標準偏差だと教える教員もいる。

• 兵庫大学の河野稔によるウェブページや神戸大学の中澤港によるウェブページでは前者である。
• 東北学院大学の根市一志による資料では後者である。

このように、同じ用語でも話者によって定義が異なる場合がある。

表計算ソフト

表計算ソフトでは次のようなワークシート関数が用意されている。

確率変数の標準偏差

離散型確率変数

X を離散型確率変数とする。X のとりうる値を x₁, x₂, …, x_n, … とし、X が x_i をとる確率を p_i で表す。このとき

${\displaystyle \textstyle \sum \limits _{i=1}^{\infty }p_{i}=1\quad (p_{i}\geq 0)}$

である。このとき

${\displaystyle E[X]=\textstyle \sum \limits _{i=1}^{\infty }p_{i}x_{i}}$

を確率変数 X の期待値という。また、

${\displaystyle V[X]=E{\Bigl [}{\bigl (}X-E[X]{\bigr )}^{2}{\Bigr ]}=\textstyle \sum \limits _{i=1}^{\infty }p_{i}{\bigl (}x_{i}-E[X]{\bigr )}^{2}=E[X^{2}]-(E[X])^{2}}$

を確率変数 X の分散という。この分散の非負の平方根を標準偏差という。

連続型確率変数

X を連続型確率変数とする。X の値が区間 [x₁, x₂] に属する確率が、連続関数 f(x) を用いて

${\displaystyle \int _{x_{1}}^{x_{2}}\!f(x)\,dx}$

と表せるとき、f(x) を X の確率密度関数という。このとき

${\displaystyle f(x)\geq 0,\quad \int _{-\infty }^{\infty }\!f(x)\,dx=1}$

である。このとき

${\displaystyle E[X]=\int _{-\infty }^{\infty }\!xf(x)\,dx}$

を確率変数 X の期待値という。また、

${\displaystyle V[X]=\int _{-\infty }^{\infty }\!{\big (}x-E[X]{\big )}^{2}f(x)\,dx}$

を確率変数 X の分散という。この分散の非負の平方根を標準偏差という。

標準偏差の推定

母標準偏差が未知のときは、標本から得られた標本標準偏差から推定することができる。母標準偏差を σ、大きさ N の標本の標準偏差を s とすると、母集団分布が正規分布ならば σ² は次の自由度 N − 1 の χ² 分布に従う。

${\displaystyle \chi ^{2}={\frac {Ns^{2}}{\sigma ^{2}}}}$

σ の95%信頼区間は P = 0.975 の χ² から P = 0.025 の χ² までの範囲で、s と σ の比は N = 5 では 0.31 から 1.49、N = 20 では 0.67 から 1.28 となり、標本が小さい場合はかなり範囲が広いことに留意すべきである。

脚注

注釈

出典

参考文献

関連項目

• 統計学
• 統計量
• 分散 (統計学)
• 偏差
• 偏差値
• 平均偏差
• 四分位偏差
• 二乗平均平方根 (RMS)
• 標準誤差 (SE)
• 正規分布
• リスク

外部リンク

• Weisstein, Eric W. "Standard Deviation". mathworld.wolfram.com (英語).
• 『標準偏差』 - コトバンク